How to use poker solvers properly
A closer look at why more complex is not always better in Poker and how to use solvers more effectively
By Brandon Wilson
While maximizing a solver’s input capabilities is a fun and useful exercise for gleaning information and discovering new generations of EV, creating overly complex game trees and attempting to execute their outputs in-game is dangerous and ineffective. In this article, we will make the case that players earn more EV by simplifying their game to what is realistically implementable individually, despite the allure of seeing a increased EV figure in the solver for more complex strategies.
Fancy solver syndrome:
how game tree complication can backfire
One common phenomenon in the current climate of solver usage is multiple sizing inputs on each street, most often on the flop. First, the problem with this: it is our view that, in general, it is virtually impossible for the vast majority of players to properly implement certain strategies they are asking (often unwittingly) their software to solve.
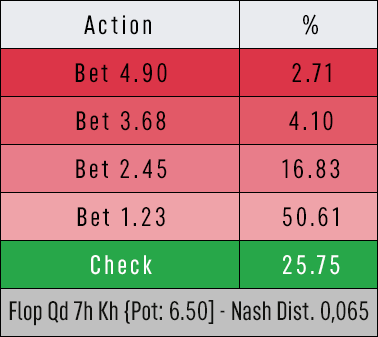
Source: “Finding Equlibrium” YouTube
One such case is asking the poker solver to create an equilibrium for, say, 4 different C-bet sizes for a common single raised pot. While this may be useful for what some would term “research,” i.e., discovering potentially previously unknown strategic preferences with regard to bet size, it is generally ineffective as a final stop strategy, per se, that one resolves to execute in-game.
The reason for this is two-fold: firstly, the difficulty of accurately mixing five actions is heightened, which leads to more costly mistakes than a strategy uses, say, 2 C-bet sizes—one large and one small. Secondly, the study problem: this 5-way flop range split often results in river ranges containing very few combinations—oftentimes 3 or even fewer. These ranges struggle to produce reliable patterns and useful takeaways, as they are not aligned with how most players would have constructed their strategies up to this node—that is, even if they wanted to.
Conversely, if we removed two sizes from this strategy to better reflect what a human might actually attempt, the output would look vastly different. The remaining sizes would be used at relatively higher frequencies, resulting in ranges that better reflect what one encounters in-game and maintain combinatorial integrity such that the sub-3-combo nodes are encountered much less frequently. Also important to note is that many simulations will not converge to the desired Nash distance if they are too complex, further damaging the reliability of the outputs. In the following example, the relatively low Nash distance is manifesting in a mix of an action that is losing 10bb in EV as compared to the best option. In sufficiently converged simulations, this would not occur.
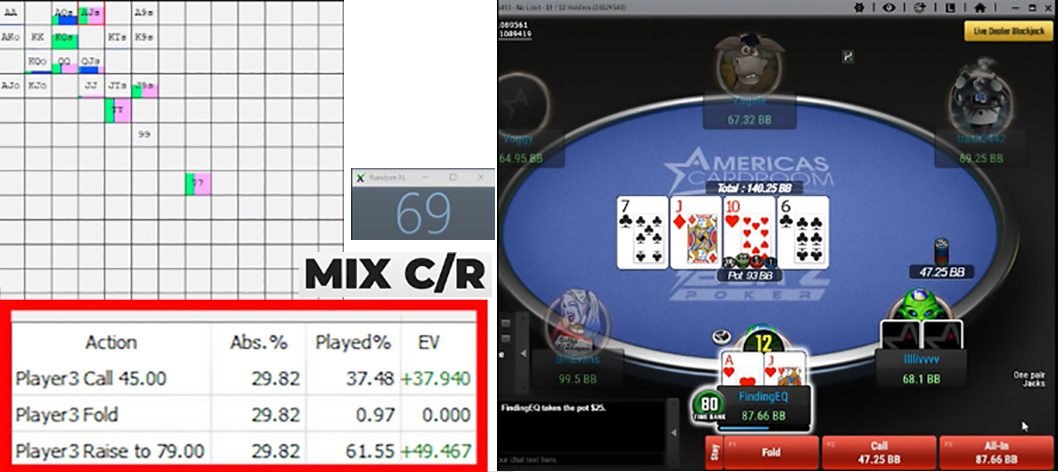
Source: “Finding Equlibrium” YouTube
Potential drawbacks to simplification and benefits of complicating game trees
Proponents of the study mechanism this article criticizes may rightfully argue that, when plugged into a solver, their more complex game tree yields more theoretical EV for the player in question than what we are suggesting, which is a simpler, “dumbed down” iteration of the tree. Our rebuttal to this type of notion would be simple. If, as we stated, a more complex tree does not converge to a sufficiently low Nash distance, the EV numbers displayed will not be as precise as a simpler simulation run closer to 0% exploitability. More importantly, however, even if we concede that the more complex strategy yields more EV in theory, this gain does not translate to real-life EV for the player if he is unable to execute the relative impossibility he has laid out for himself.
The other side may also use some form of “speak for yourself” rhetoric with regard to execution. That is, perhaps we cannot execute what they’ve set forth, but they can. They may even provide examples of players who have succeeded using a more complex approach. Firstly, while there may be players executing closely enough at the far-right end of the poker skill bell curve to make such an approach worthwhile, these would be the exception—if they exist. Therefore, it is far from earnest or even useful, then, to be touting such approaches as valid strategy advice for the poker world at large.
The reality is human brains are not supercomputers, and are yet lesser saps than that when compelled by the time restraints of an action clock. It is unwise and detrimental to a player’s expectation to put more time into studying strategies he absolutely cannot replicate versus ones with which he has a fighting chance.
The correct approach, then, is to tailor one’s solver study to what she deems most close to feasible for her capability of execution. There is no one-approach-fits-all with respect to this feasibility, but if there were, it certainly would not be the most complicated available.
DTO Poker brings you accurate results of poker solvers directly to your phone or desktop
Finally, this is why DTO exists. It makes studying robust and implementable strategies accessible to any player, and it is the obvious option for players who prefer not to learn solvers or to run their own sims. It is meant to be a tool whose use results in growth in pattern recognition and equilibrium mechanics and consequently visible gains in win rate.
About the author
Brandon Wilson is an American poker player and writer. He earned his Journalism degree from Northwestern University’s Medill School of Journalism, and after spending three years in the field, found poker. He credits DTO as instrumental to his improvement and uses the tool regularly. Outside of the game, Brandon teaches yoga and serves as a mentor for high school students for the Daniel Murphy Scholarship Foundation.